背景介绍

脑电一般指大脑皮层的连续节律性变化，广泛用于神经科学研究、临床诊断和治疗等领域。科研人员根据频率可以将脑电分为四种：α波、β波、θ波、δ波，不同的脑电波代表了人体不同的精神状态：当人们处于比较紧张的情况时，人脑中能够检测到更多的 β 波；变得瞌睡的时候，会检测到更多的 θ 波；睡眠比较深入的时候，检测到的主要是 δ 波；而处于比较轻松的状态，脑袋也比较灵活，出现α波。

脑电信号处理

脑电采集过程中会不可避免地引入各种噪声，主要包含生物电噪声和环境噪声两种。其中，生物电噪声主要包含心电、肌电和眼电等；环境噪声主要包含工频干扰、电子噪声以及电极接触不良引起的噪声等，我们可以通过滤波器、独立成分分析（ICA）等方式进行预处理。

小波变换

工程中能够通过Fourier 变换将传感器采集的数据转化到频域，进而获取隐含的数据价值。该方法广泛应用于信号滤波、图像增强以及音视频处理等领域。然而实践中发现，Fourier变换不具备局部化分析能力、不能分析非平稳信号（地震信号、脑电信号）等。

调研发现，脑电信号一般采用小波分析来提取信号特征，具体的数学原理为：假定 s ( t ) 是一个变量为时间 t 的连续函数，那么他的小波变换就可以表达为：

小波变化的具体过程为：将信号通过不同频率的滤波器，分别得到高频和低频两种分量。将每一层高通滤波后得到系数称为细节系数，低通后得到的系数称为近似系数。其中，低频成分蕴含着序列的特征，高频成分可以给出序列变化的细节。

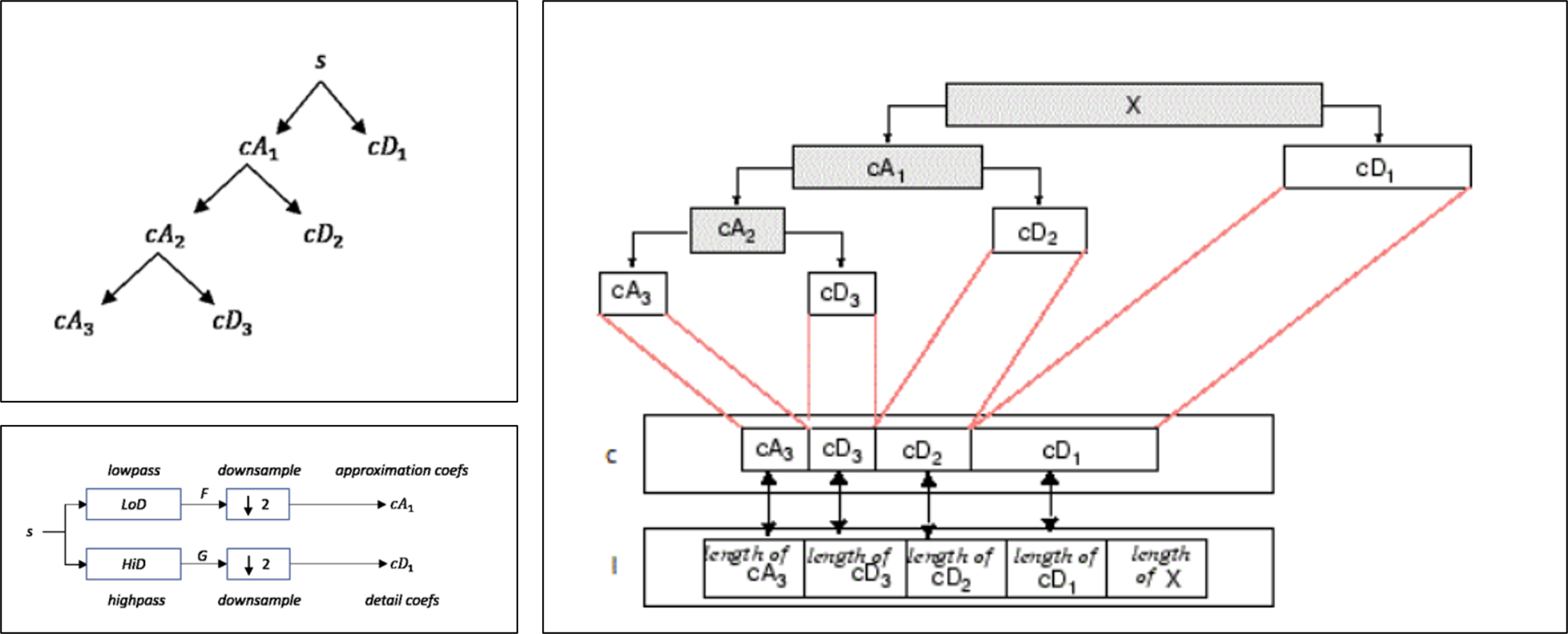
小波变换中主要的参数主要包含小波类型和分解层数两种。调研相关资料发现，小波函数主要有 Haar 小波、Morlet 小波、Daubechies（DB）小波等，使用过程中需要依据应用场景进行动态调整。分解层数一般依据信号的采样频率，分辨率以及计算量大小等。

小波包变换

当我们采用小波变换时，我们很难求取Alpha波的能量（频率范围为9-14Hz），我们只能采用D5（8-16Hz）来近似替代，该方法具有一定的误差。因此我们可以采用小波包分解的方法，设置足够的分解层数，后续通过重构获取目标频率的信号。

小波包分解层数的选择：项目中我们采用美国神念推出的脑电芯片，其采样频率为512Hz；考虑到信号四个节律的频率范围： delta波0-4Hz、 theta波4-8Hz、 alpha波8-14Hz（和 beta波14-30Hz（本实验分解得到的子带应包含以上四个频段。由于信号的有信息主要集中在低频段部分，故分解层数不能过低，但随着分解层数增加的同吋分解过程中的计算量和复杂程度也大大增加。因此，当EEG信号的釆样频率 在512hz吋，为了满足频率分辨率的要求，本文最终选择的分解层数为7层，最小的频率分辨率为 2 Hz。具体用的程序算法为：

wpt = wpdec(shuju,7,'db4','shannon');

ee=wenergy(wpt);
xiaobochangdu=2^7;
# plot(wpt)
# Read packet coefficients. 

for m=1:1:xiaobochangdu
  temp=[7,m-1];
  cfs(m,:) =wpcoef(wpt,temp);
end

subplot(211); 
plot(cfs(1,:)); title('Packet (7,0) coefficients');

# Reconstruct packet 
for m=1:1:xiaobochangdu
  temp=[7,m-1];
  rcfs(m,:) =wprcoef(wpt,temp);
end
subplot(212); 
plot(rcfs(1,:)); title('Reconstructed packet (7,0)');

fs=512

f_fft=fft(shuju);
N=length(f_fft);%这里取出f_fft也就是信号做完fft之后的序列长度
 
Y=f_fft(1:N/2+1);
Y(2:end-1)=2*Y(2:end-1);
 
Y_amp=abs(Y)/N;
 
df=fs/N;
 
f=(0:1:N/2)*df;
subplot(312);
plot(f,Y_amp)